Př. 1.

a) Namodelujte situaci ryby - rybáři, kdy se vzrůstajícím počtem rybářů klesá počet ryb. Ovšem, jakmile je rybářů příliš a ryb málo, začne klesat počet rybářů a tedy opět vzrůstat počet ryb.

b) Zkuste najít ideální počet rybářů a ryb, který vytvoří rovnováhu (rybáři nemusí přicházet/odcházet a ani ryby se nepřemnoží/nevyhynou).

ad a)Využijeme model Lotka-Voltera

dx/dt = alfa . x(t) - beta . x(t) . y(t) (rovnice pro kořist)

alfa - exponenciální nárůst kořisti (uvažujeme neomezené krmivo, místo k žití atd.)

beta - úbytek vlivem predátora

dy/dt = delta . x(t) . y(t) - lambda . y(t) (rovnice pro predátora)

Uvažujme natalitu (porodnost - tj. přirozený přírůstek) ryb 1,5 a úmrtnost (mortalitu) 0,5.

U rybářů srovnatelně míra příchozích - 0,4 a míra odcházejících 0,8. Pak:

alfa=1.5;
beta=0.5;
gama=0.8;
delta=0.4;

Uvažujme na začátku 8 ryb a 8 rybářů v časovém intervalu 10 časových jednotek (dní):

x0=[8,8]; tn=10;

x označím jako x(1) a y jako x(2) a dosadím lotka-volterrovy rovnice do anonymní fce:

f=@(t,x)[alfa*x(1)-beta*x(1)*x(2); delta*x(1)*x(2)-gama*x(2)];

Vyřeším rovnice pomocí ODE45. To jak dlouho rovnice trvá vyřešit, zjistím pomocí příkazů tic a toc (měří se doba vykonání kódu mezi nimi, která se pak automaticky vypíše):

tic, [t,x] = ode45(f,[0,tn],x0), toc;

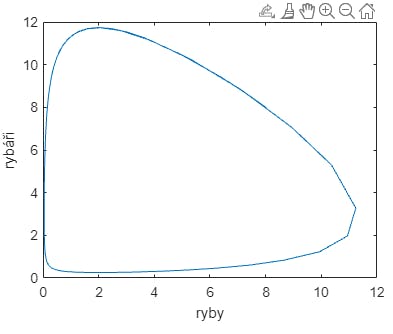
Nyní si zobrazím graf:

plot(x(:,1),x(:,2)), xlabel ryby, ylabel rybáři

Celý kód:

alfa=1.5;
beta=0.5;
gama=0.8;
delta=0.4;
x0=[8,8]; tn=10;
f=@(t,x)[alfa*x(1)-beta*x(1)*x(2); delta*x(1)*x(2)-gama*x(2)];
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2)), xlabel ryby, ylabel rybáři

Graf:

Pokud bych chtěl vidět, jak se postupně mění počet ryb/rybářů, místo příkzu plot využiji comet:

comet(x(:,1),x(:,2));

Pozn.: V ukázce si můžeme všimnout, že počet ryb je v určitém momentu blízko k nule (graf se je daleko více blíže k y-ové nežli k x-ové ose). V praxi by tato oblast znamenala vyhynutí ryb a v důsledku i vymizení rybářů (tzv. atto-fox problem - podle situace, kdy zbude 10^(-18) lišky - v praxi by opět druh vyhynul).

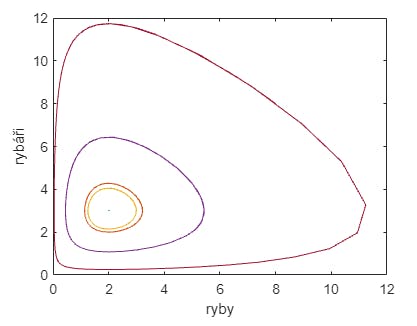
ad b) Hledám optimální situaci.

Podržím si graf pomocí hold on a do toho stejného zadám jinou počáteční hodnotu. Zjistil jsem, že pokud zadám hodnotu [2,3], vychází bod => vytvořila se rovnováha (znamená to tedy, že v moři budou plavat dvě ryby a chytat je 3 rybáři):

hold on 

x0=[2,3.01]; 
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2))

Celý kód (včetně hledání dalších možností):

alfa=1.5;
beta=0.5;
gama=0.8;
delta=0.4;
x0=[8,8]; tn=10;
f=@(t,x)[alfa*x(1)-beta*x(1)*x(2); delta*x(1)*x(2)-gama*x(2)];
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2)), xlabel ryby, ylabel rybáři
hold on 

x0=[2,3.01]; 
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2))
hold on

x0=[2,2]; 
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2))
hold on

x0=[3,3]; 
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2))
hold on

x0=[5,2]; 
tic, [t,x] = ode45(f,[0,tn],x0), toc;
plot(x(:,1),x(:,2))
hold on

Graf: